两点之间不包含任何点的最宽垂直区域

题目

---

给你 n 个二维平面上的点 points ，其中 points[i] = [xi, yi] ，请你返回两点之间内部不包含任何点的 最宽垂直区域 的宽度。

垂直区域 的定义是固定宽度，而 y 轴上无限延伸的一块区域（也就是高度为无穷大）。 最宽垂直区域 为宽度最大的一个垂直区域。

请注意，垂直区域 边上 的点 不在 区域内。

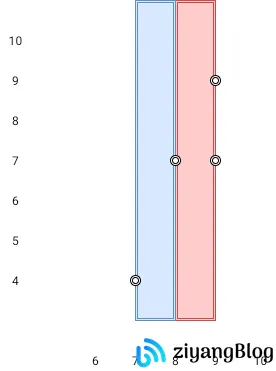
示例 1：

输入：points = [[8,7],[9,9],[7,4],[9,7]]
输出：1
解释：红色区域和蓝色区域都是最优区域。

示例 2：

输入：points = [[3,1],[9,0],[1,0],[1,4],[5,3],[8,8]]
输出：3

提示：

• n == points.length
• 2 <= n <= 105
• points[i].length == 2
• 0 <= xi, yi <= 109

分析题目

---

这道题使用朴素法解，并不复杂，但题目写的确实很让人难以理解，所以重新翻译了一下题目：

给出二维平面上的 n 个点，其中 point[i]=[xi, yi]，返回 两点之间最宽的垂直区域，使得没有任何点在该区域内。

垂直区域是一个沿Y轴无限延伸的固定宽度的区域（即无限的高度）。最宽的垂直区域是具有最大宽度的区域。

请注意，位于垂直区域边缘的点不被视为包括在该区域内。

思路

那么根据上述题意，我们可以知道这道题想要求得的是： 在 x 轴中两个相邻点位大最大宽度。

为什么是相邻点位？因为题目要求是两点之间不允许有其他点位存在，所以两点之间必然是相邻的。

那么我们只需要根据 x 点位进行排序后，取得 $max[x_i - (x_i-1)]$ 即可

具体实现

---

Java 实现

class Solution {
 public int maxWidthOfVerticalArea(int[][] points) {
  Arrays.sort(points, (a, b) -> a[0] - b[0]);
  int res = 0;
  for(int i = 1; i < points.length; i++){
   res = Math.max(res, points[i][0] - points[i - 1][0]);
  }
  return res;
 }
}

JavaScript 实现

var maxWidthOfVerticalArea = function(points) {
 points.sort((a, b) => a[0] - b[0]);
 return points.reduce((total, cur, idx) => {
  if(idx == 0) return 0;
  return Math.max(total, cur[0] - points[idx - 1][0]);
 },0);
};

复杂度分析

• 时间复杂度：$O(n\ log\ n)$，其中 n 是输入数组的长度，排序消耗 $O(n\ log\ n）$时间复杂度。
• 空间复杂度：$O(log\ n)$，为排序的空间复杂度。