题目 给定一个长度为 n 的链表 head
对于列表中的每个节点,查找下一个更大节点 的值。也就是说,对于每个节点,找到它旁边的第一个节点的值,这个节点的值严格大于 它的值。
返回一个整数数组 answer ,其中 answer[i] 是第 i 个节点(从1开始 )的下一个更大的节点的值。如果第 i 个节点没有下一个更大的节点,设置 answer[i] = 0 。
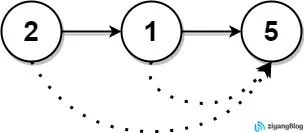
示例 1:[2,1,5][5,5,0]
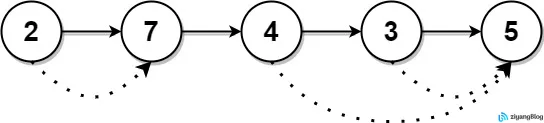
示例 2:[2,7,4,3,5][7,0,5,5,0]
提示:
链表中节点数为 n1 <= n <= 1041 <= Node.val <= 109
分析题目 这是一道比较常见的 NGE问题 (Next Greater Element),这道题的主要是求相邻最大值的数组,也就是说从下标 0 开始,寻找相邻最近大于当前的值,找到了,就将当前的值改为当前最大值,如果一直到数组结束也没有比他更大的,则将设置为 0。
方法1:暴力枚举 思路 这类问题,暴力枚举一定是可以解决问题,但时间复杂度会很高。
其核心思路也很简单,每一个下标,当从当前位置遍历到最后,查找有没有比当前大的值,有则更新,无则置为0。
具体实现 Java 实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public int [] nextLargerNodes(ListNode head) {new ArrayList <>();while (head != null ){ListNode cur = head.next;int val = 0 ;while (cur != null ) {if (cur.val > head.val){break ;return list.stream().mapToInt(i -> i).toArray();
JavaScript 实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 var nextLargerNodes = function (head ) {const ans = [];while (head){let cur = head.next ;let val = 0 ;while (cur) {if (cur.val > head.val ){val ;break ;next ;push (val);next ;return ans;
复杂度分析
时间复杂度:$O(n^2)$ , 其中 n 是链表的长度, 因为需要嵌套两层循环,所以时间复杂度为 $O(n^2)$
空间复杂度:$O(n)$ , 其中 n 是链表的长度,由于变量 cur 只保存了 head 的指针,没有申请额外的空间,所以 cur 的空间复杂度为 $O(1)$
方法2:单调栈 思路 单调栈是一种和单调队列类似的数据结构。单调队列主要用于解决滑动窗口问题,单调栈则主要用于解决NGE 问题。
单调栈的主要解题思路就是,通过维护一个栈,表示“待确定NGE的元素”,然后遍历序列。当我们碰上一个新元素,我们知道,越靠近栈顶的元素离新元素位置越近。所以不断比较新元素与栈顶,如果新元素比栈顶大,则可断定新元素就是栈顶的NGE,于是弹出栈顶并继续比较。直到新元素不比栈顶大,再将新元素压入栈。
具体实现 Java 实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution {public int [] nextLargerNodes(ListNode head) {new ArrayList <>();int []> stack = new Stack <>();int idx = 0 ;while (head != null ){0 );while (!stack.isEmpty() && stack.peek()[1 ] < head.val) {0 ], head.val);new int []{idx, head.val});return list.stream().mapToInt(i -> i).toArray();
JavaScript 实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 var nextLargerNodes = function (head ) {const ans = [];const stack = [];let idx = 0 ;while (head){push (0 );while (stack.length && stack[stack.length -1 ][1 ] < head.val ) {splice (stack.pop ()[0 ], 1 , head.val );push ([idx, head.val ]);next ;return ans;
复杂度分析
时间复杂度:$O(n)$ , 其中 n 是链表的长度,对链表进行遍历需要 $O(n)$的时间,链表中的每个元素恰好入栈一次,最多出栈一次,这一部分的时间也为 $O(n)$。
空间复杂度:$O(n)$ , 其中 n 是链表的长度, 即为单调栈需要的空间。